어린이과학동아&수학동아 기사
10억 원을 버는 가장 어려운 방법, 밀레니엄 문제
(ㅊㅊ: 위키피디아)
이 세상에는 수많은 문제와 가설들이 있습니다.
물론 지금까지 풀리지 않은 문제도 굉장히 많죠.
이번 기사에서는 현재 세계에서 가장 어려운 문제로 꼽히고 있는 7개의 문제들을 소개해 드리겠습니다.
일단 이 문제들은 세계의 많은 저명한 학자들이 뽑은 7가지의 문제로,
'밀레니엄 문제' 라 부릅니다
솔직히 저도 보면서 이해 못했던 부분이 정말 많았기 때문에,
자세히는 아니고 간단히 7가지의 문제를 알아보겠습니다.
밀레니엄 문제에는 7개의 문제가 포함되어 있습니다.
나비에-스토크스 방정식, 리만 가설, P-NP 문제, 양-밀스 가설, 호지 추측, 버츠와 스위너톤-다이어 추측,
그리고 푸앵카레 추측이 있습니다.
1. 일단 이 중에서 유일하게 돌파된 문제는 푸앵카레 추측입니다.
이 문제는
3차원 공간에서 모든 닫힌 곡선(폐곡선)이 하나의 점으로 모일 수 있다면 그 공간은 구로 변형될 수 있다
|
라는 가설인데요
쉽게 풀어서 말하면 어떤 공간에 있는 닫힌 곡선들이 모두 한 지점으로 모일 수 있다면,
그 공간을 구의 형태로 변하게 할 수 있다는 겁니다
예를 들어 어떠한 공간 가운데에 기둥이 길게 있다고 칩시다
위에서 보면 이런 모양인 거죠

그럼 여기의 한 지점에서 아무 곳에다 줄을 날려보냅니다
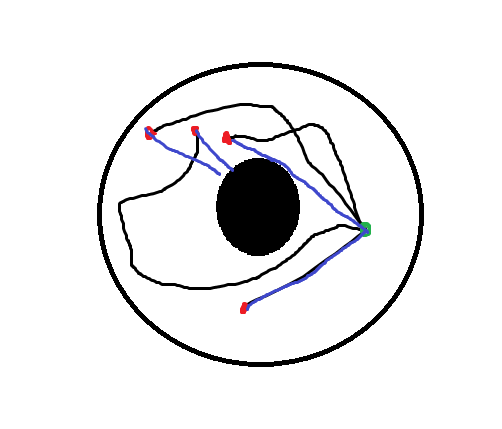
그렇게 되면 위의 그림처럼 줄의 끝부분과 시작지점을 직선으로 이었을 때
어떤 선은 가운데 기둥에 막히게 됩니다.
그러니 이건 구 모양으로 만들 수 없죠.
다만 구 모양의 공간은 막히는 장애물이 없으니
만약 어디로 줄을 던지든 막히지 않는다면,
그건 구가 될 수 있다라는 가설입니다
그리고 이 문제는 2000년대 그레고리 페렐만이라는 수학자에 의해 증명되었습니다.
2. 나비에-스토크스 방정식
이 문제는 기본적으로 수학 문제라서 이해가 어렵습니다
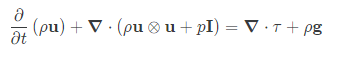
이 방정식이 성립하는가 하는 문제죠
저 용어들은 잘 모르겠지만
일단 이 방정식을 구했을 때 이게 지금 이 세상을 대입했을 때 무조건 답이 있냐.. 하는 문제입니다
그래서 틀린 답을 하나만 구해도 그게 증명한 거에요
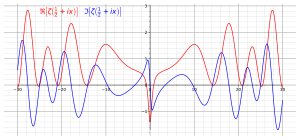
3. 리만 가설
이 가설은 풀어서 설명하면 이렇습니다.
1을 제외한 모든 자연수를 소인수분해합니다.
그리고 여기에 같은 소수가 두 번 이상 들어간 수는 제외합니다.
그럼 만약에 소인수가 짝수면 1, 홀수면 0을 대입합니다.
2는 0(2) 3은 0(3) 6은 1(2x3), 8은 제외(2x2x2)
이렇게요.
그러면 이렇게 했을때, 아무 자연수를 골라서 소인수분해하면 짝수나 홀수가 나올 확률은
50대 50으로 같다는 가설입니다.
이 문제를 증명하려면
이게 맞는 말이다, 이게 틀린 말이다,
아니면 이 문제는 풀 수가 없다!
중에 하나와 그 이유를 알아내야 합니다.
4. 버츠와 스위너톤-다이어 추측
수체(number field) KK 위에서의 타원곡선 EE의 모델-베유 군(Mordell-Weil group) E\left(K\right)E(K)의 계수(rank)는, EE의 하세-베유 LL-함수(Hasse-Weil L-function) L\left(E,s\right)L(E,s)가 s = 1s=1에서 갖는 근의 차수와 같다.
넘어갑시다.
애초에 제 머리로 이해도 못했어요
5. 양-밀스 가설
임의의 콤팩트하고 단순한 게이지 군(compact simple gauge group) G에 대해서, \mathbb{R}^4R4상의 자명하지 않은 양-밀스 이론이 존재하여, Δ > 0 인 질량 간극을 가짐을 증명하시오. 존재의 증명은 적어도 몇몇 논문에 인용한 것만큼 강한 공리적 체계를 구성하는 것을 포함해야 한다.
이게 뭐냐면 세상에 존재하는 모든 입자들은 무게가 있을까? 라는 문제입니다.
넘어가죠.
6. 호지 추측
이거는 설명 못합니다
대수기하학이라는 대학과정을 알아야 이해를 할 수가 있어요
물론 저는 모릅니다
7. P-NP 문제
P 문제는 다항식 시간(어떤 문제를 푸는데 걸리는 시간의 최대치가 x에 대한 방정식인 것)
(즉 어떤 방정식의 답이 식을 푸는데 걸리는 최대 시간인 것)
다항식 시간 안에 답을 확실히 알 수 있는 문제,
NP 문제는 다항식 시간 안에 답이 맞는지 알 수 있는 문제인데요
이 두 개가 서로 같은 것인지 다른 것인지를 증명하는 문제입니다.
그니까 대충 문제가 푸는데 쉬우면 검산할 때도 쉬울까 하는 문제입니다.
지금까지 김민석 기자였고요,
솔직히 이거 너무 난해해서 보류될 것 같다는 생각이 많이 드네요
글쓰기 평가어린이과학동아 기자2022.02.09
밀레니엄 문제를 소개하는 주제로 글을 쓴 점 자체가 놀랍고, 박수를 보냅니다. 사실 각각의 문제를 이해하는 것조차도 일반인도 어려운데요, 이 글을 읽어 보니까 그래도 민석 친구가 수학에 대한 관심과 이해 정도가 무척 높다는 생각이 드네요. 몇 가지 문제를 자신이 이해하고 자신의 말로 설염한 것을 알 수 있었어요. 뒤에 있는 문제는 정말 수학 전공자도 이해하기 어려운 문제니까 그런 문제를 소개하려 하기 보다는 앞 부분에 그나마 조금이라도 이해할 수 있는 것들만 소개해도 괜찮을 것 같아요. ^^

잘 정리하셨어요~
마지막으로