어린이과학동아&수학동아 기사
삼각형의 내각의 합이 180도가 아니라고?!
안녕하세요. 윤보연 기자입니다. 여러분은 '유클리드 기하학'에 대해 들어보셨나요? 이번 기사로는 '유클리드 기하학'과 반대되는 '비유클리드 기하학' 중 하나인 '구면기하학'에 대해 알아보겠습니다. 일단 '유클리드 기하학'과 '비유클리드 기하학'이 뭔지 모르시는 분들을 위해 그게 무엇인지 먼저 설명하고 '구면기하학'에 대해 알아보도록 하겠습니다.
1. '유클리드 기하학'

'유클리드 기하학'이란 고대 그리스 수학자인 에우클레이데스(유클리드, Euclid)가 정립한 최초의 기하학입니다. 이 '유클리드 기하학'에는 5가지의 공리가 있습니다. 5가지 공리의 내용은 이러합니다.
1. 서로 다른 두 점이 주어졌을 때 그 두 점을 지나는 직선을 그릴 수 있다.
2. 임의의 선분은 더 연장할 수 있다.
3. 서로 다른 두 점 A, B에 대해 A를 중심으로 선분 AB를 반지름으로 하는 원을 그릴 수 있다.
4. 모든 직각은 서로 합동이다.
5. 한 선분을 서로 다른 두 직선이 교차할 때, 두 내각의 합이 180도보다 작으면,
이 두 직선을 연장할 때 두 내각의 합이 180도보다 작은 쪽에서 교차한다.
5번째 공리는 자세히 알려드리도록 하겠습니다.
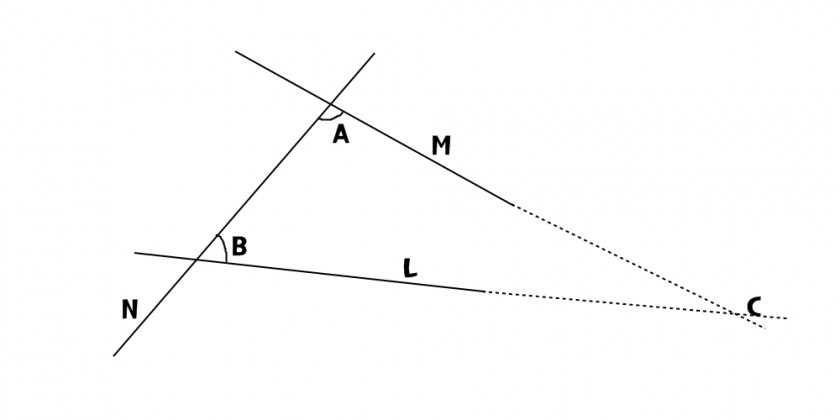
위의 사진에서 직선 N에 두 직선 M과 L을 교차했을 때 생기는 각을 각각 A, B라 하겠습니다. 이 때 각 B가 각 A보다 작기 때문에 두 직선 M과 L에 연장선을 그려 점 C로 만나게 하면 점 C는 더 작은 각(각 B)을 가지고 있는 직선 L쪽으로 치우치게 됩니다. 이게 바로 5번째 공리입니다.
이 기하학은 무려 2000년 동안 널리 쓰이며 '절대 진리'로 여겨졌다고 합니다. 하지만 19세기 새로운 기하학이 등장하게 됩니다. 그게 바로 '비유클리드 기하학'입니다.
2. '비유클리드 기하학'
'비유클리드 기하학'이란 가우스, 보여이, 로바체프스키 등에 의해 등장하게 된 기하학입니다. 이 기하학 속에는 '쌍곡 기하학'과 '구면 기하학'이 있습니다. 이 기하학은 '유클리드 기하학'의 5번째 공리 등이 성립하지 않는 상황이 있다는 걸 증명합니다. 이 '비유클리드 기하학'은 아인슈타인의 '상대성 이론'과 대단한 연관이 돼 있습니다.
3. '구면기하학'

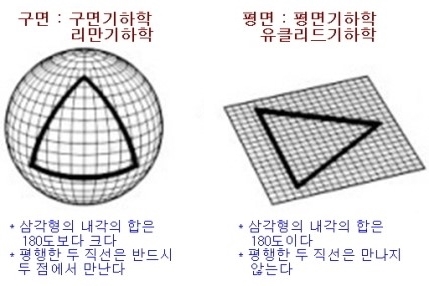
'구면기하학'은 수학자 리만에 의해 등장하여 '리만 기하학'이라고도 불립니다. 이 기하학은 평면이 아니라 구면 위에서 여러 도형의 성질을 다룹니다. 이 '구면 기하학'으로 인해 우리가 현재 알고 있는 상식이 모순이라는 걸 증명합니다. 그럼 어떤 것이 모순인지 설명해드리겠습니다.
첫 번째, 삼각형의 내각의 합에 대한 모순입니다. 초등학교와 중학교 과정에서는 삼각형의 내각의 합은 180도라고 설명합니다.
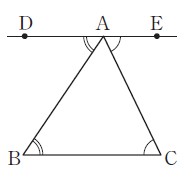
(중학교 과정에서는 위의 사진처럼 '엇각'이라는 개념을 이용해서 삼각형의 내각의 합이 180도라는 걸 증명합니다.)
하지만 구면 위에서는 다릅니다.
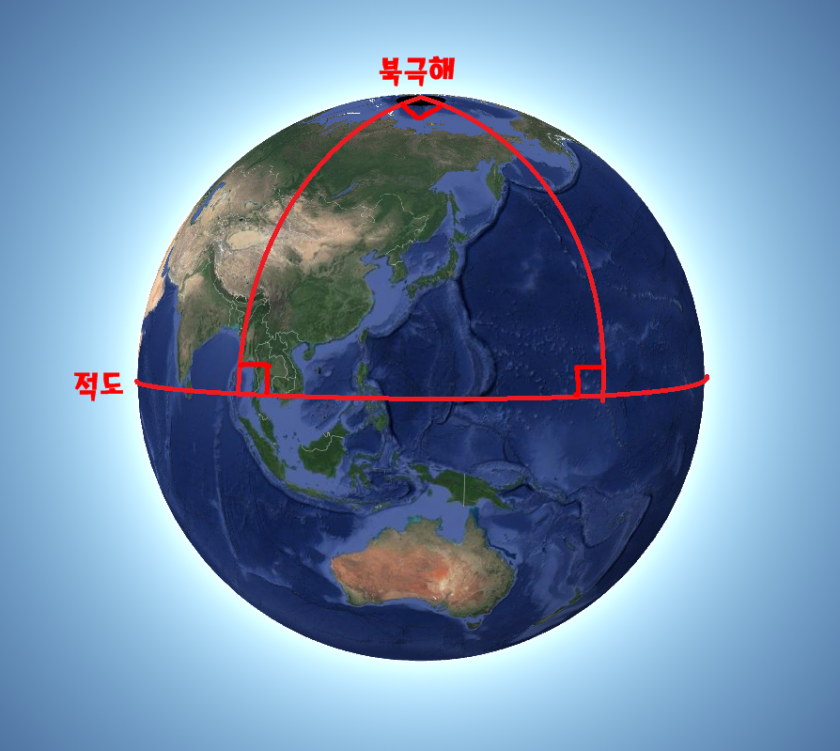
위의 사진처럼 적도에서 북극해로 선분을 그으면 한 내각의 크기가 90도가 되어 90X3으로 내각의 크기의 합이 270도가 됩니다.
두 번째, 최단거리에 대한 모순입니다. 중학교 과정에서는 두 점 A,B의 최단거리는 직선이라고 되어 있습니다. 하지만 구면 위에서는 곡선이 최단거리가 될 수 있습니다.
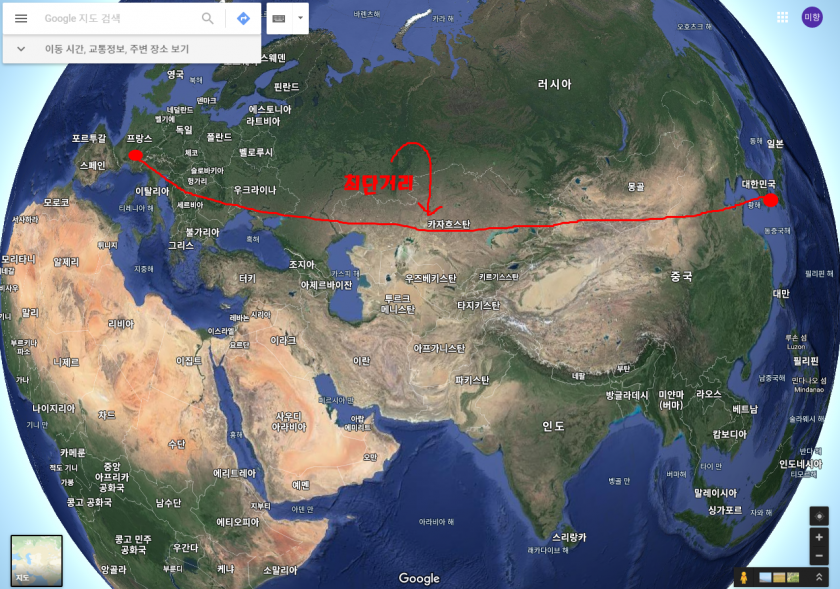
지구본 상에서 프랑스와 한국의 최단거리는 위 사진과 같습니다. 하지만 이 최단거리를 평면인 지도에 표현하게 된다면
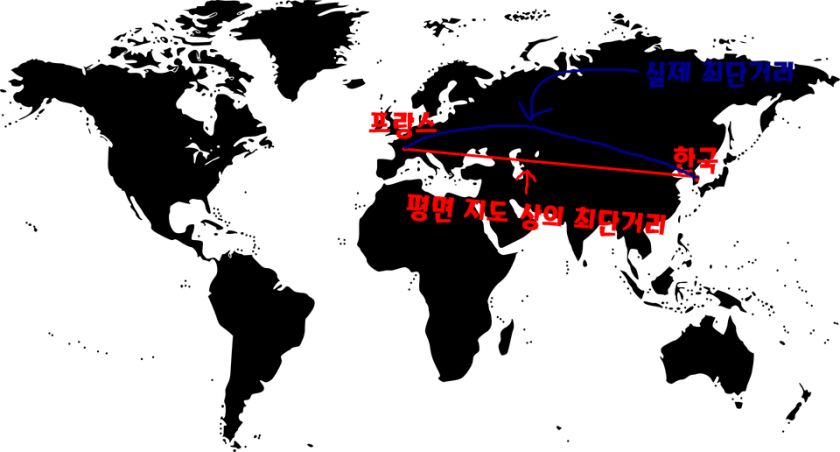
이렇게 곡선이 됩니다.
관련 동영상: https://youtu.be/4_kGXlUyfbI?t=358
세 번째, 평행선에 대한 모순입니다. 초등학교, 중학교 과정 모두 평행한 두 직선은 절대로 만나지 않는다고 되어 있습니다. 하지만 구면 위에서는 만납니다.
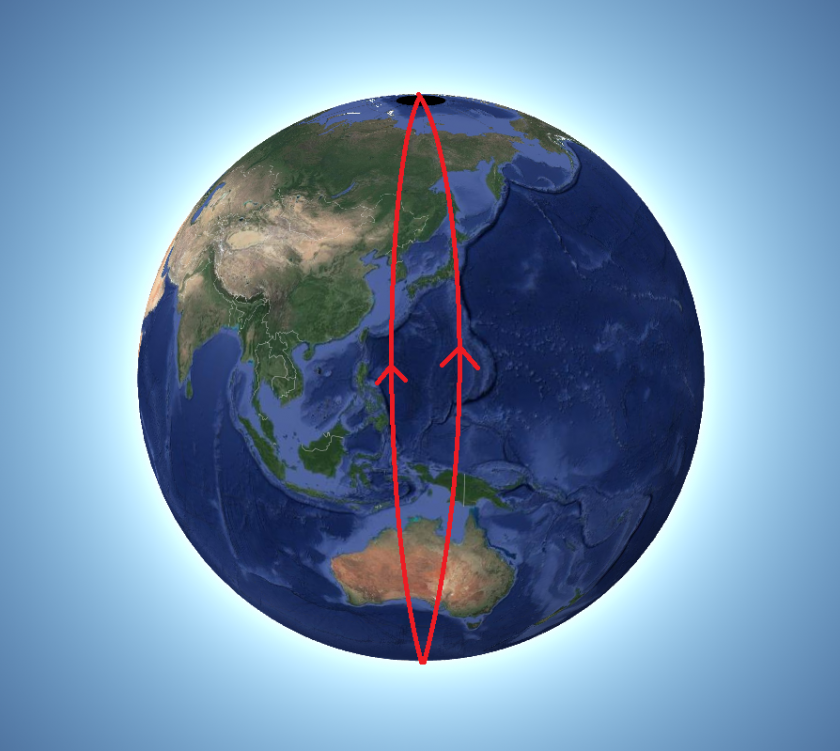
위 사진과 같이 지구본(구면) 위의 평행선은 이렇게 만나게 됩니다.
네 번째, '피타고라스의 정리'에 대한 모순입니다. '피타고라스의 정리'는 중학교 2학년 때 나오는 개념입니다.
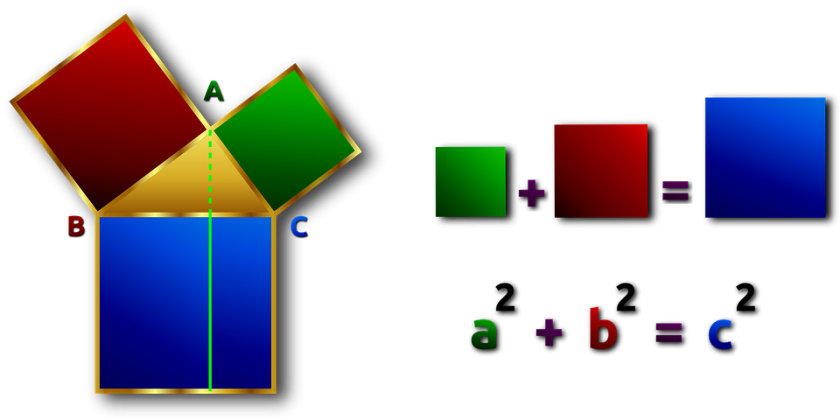
'피타고라스의 정리'란 직각삼각형에서 직각을 낀 두 변의 길이를 각각 a, b라 하고, 빗변의 길이를 c라 하면 a2+b2=c2이 성립한다는 거입니다.
하지만 이 위대한 발견은 구면 위에서는 모순이 됩니다.
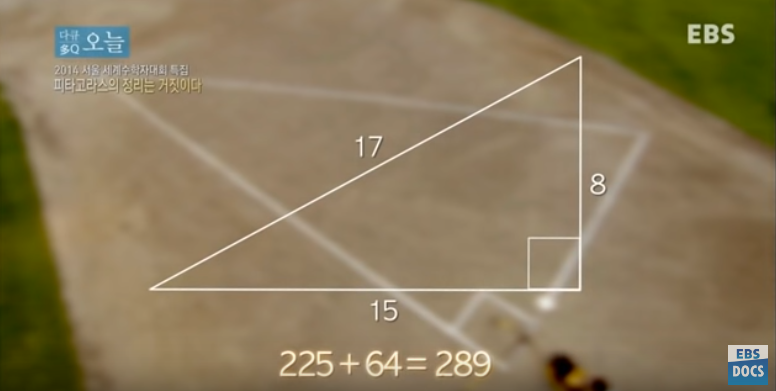
'피타고라스의 정리'는 지구(구면) 위의 작은 공간에서는 직각삼각형을 그렸을 때 식이 성립하지만
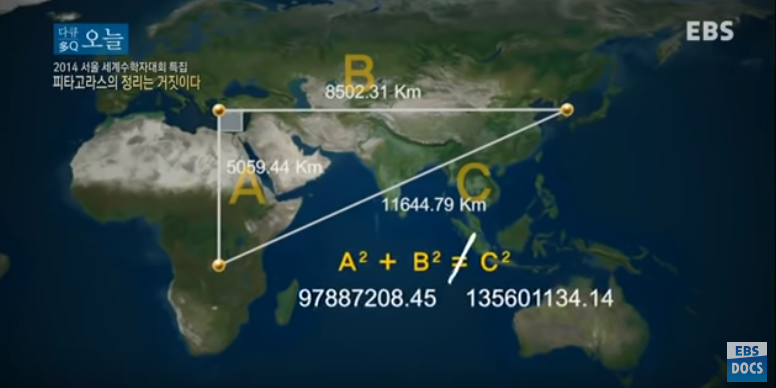
범위가 커지면 오차가 생깁니다.
관련 동영상: https://youtu.be/gWh9vw53RBk
마지막으로 정리를 하자면
라고 기억해주셨으면 좋겠습니다.
출처-픽사베이, 구글 지도, 관련 동영상 캡쳐 짤 (직접 그림판과 포토**이프로 편집한 사진도 있습니다.)
(글쓴이가 중학교 1학년이어서 고등학교 과정에 대해는 잘 모릅니다. 그래서 초등학교와 중학교 과정만 언급했습니다.)
(이 글을 쓸 때 수학동아의 기사를 참고했습니다.)
이 기사를 읽어주셔서 감사합니다.
사진, 동영상 링크가 삭제될 수도 있으니 온전한 글을 보실려면 제 블러그 링크를 눌러주세요.
https://blog.naver.com/octoberfish/221502113892
글쓰기 평가어린이과학동아 기자2019.04.02
보연 기자, 반가워요. 수학 기사를 써 주었네요. ^^ 다소 어려울 수 있는 '구면기하학'을 주제로 한 글인데, 여러 가지 자료를 참고한 흔적이 보여요. 어과동 친구들에게 구면기하학 기사가 너무 어렵지 않을까 생각이 되는데, 글에서 그림과 예시를 들어 설명한 점이 좋았어요. 구면기하학을 설명하는 참고자료에서 저런 예를 든 경우가 많아요.
출처를 잘 밝혀준 점도 좋았고, 쉽지 않은 수학 기사를 쓴 점도 흥미로웠어요. ^^ 앞으로도 활발한 활동 기대할게요. 기사 잘 봤어요.

(나만 모르는 건가..............)
신기해요!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
모를수도 있어요....:: 잘난척은 하지 말아주세요. 모르는 사람 입장에서는 기분이 안 좋아요.
님이 다 아시는건 그냥 속으로만 생각해주심 좋겠네요.
- 1
- 3
- 4
다음 마지막으로