어린이과학동아&수학동아 기사

안녕하십니까? 세종시 이우혁 기자입니다.

이번에는 마방진에 대해서 한번 알아보도록 하겠습니다.

마방진이란? 마방진은 가로 세로 대각선에 있는 수들의 합이 모두 같도록 정사각형의 연속된 수들을 한 번씩 나열한 것입니다. 누가 만들었는지는 정확히 모르지만 중국의 한나라 우황 때 거북이 등의 무늬 낙서로 시작되었다고 합니다. 마방진은 같은 길의 수 합이 다 같기 때문에 많은 사람들이 연구해 왔습니다. 모양에 따라 육각진, 팔각진 등 다양한 종류가 있습니다.

서양의 최초 마방진은 독일 딜러의 마방진입니다. 관뚜껑에 그림을 그렸는데 그것이 최초의 4차 마방진입니다.

일단 마방진을 푸는 방법을 알아보도록 하겠습니다. 마방진은 홀수마방진과 짝수 마방진으로 나타낼 수 있는데요~

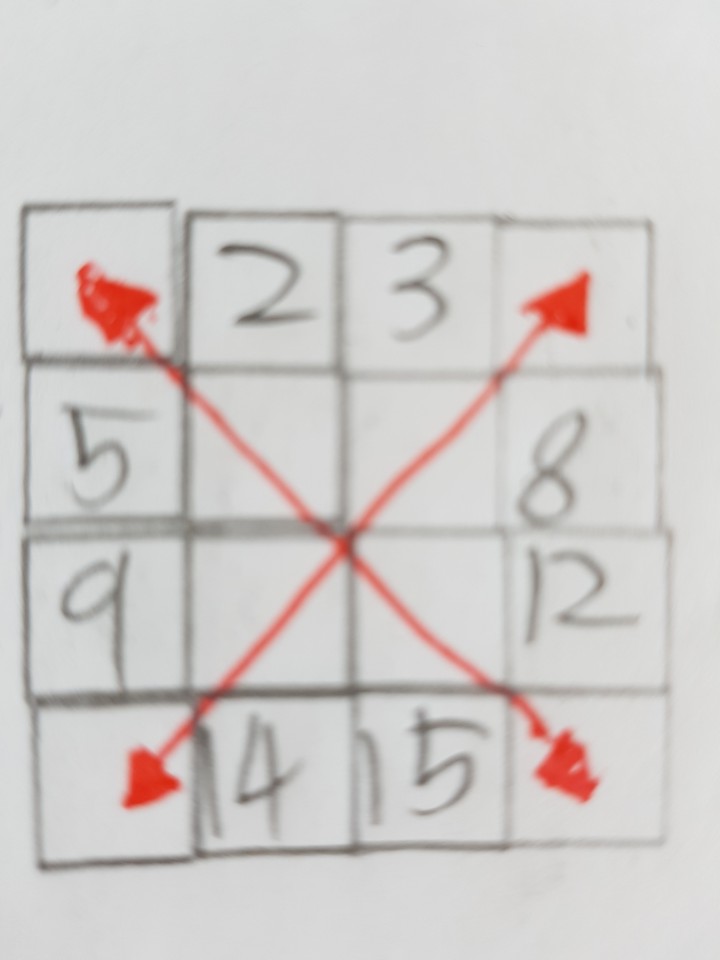
우선 홀수 마방진은 계단식으로 풀 수 있습니다. 칸이 홀수인 마방진을 만들고 대각선으로 경사진 방진을 만들고 두 번째 오른쪽 아래로 순서대로 수를 써넣습니다. 방진밖에 있는 수는 좌는 우로 우는 자로 상은 하로 하는 상으로 돌립니다. 홀수 칸만큼 평행이동 시키면 다음과 같이 됩니다.

이렇게 하면 얼마든지 마방진을 만들 수 있습니다.

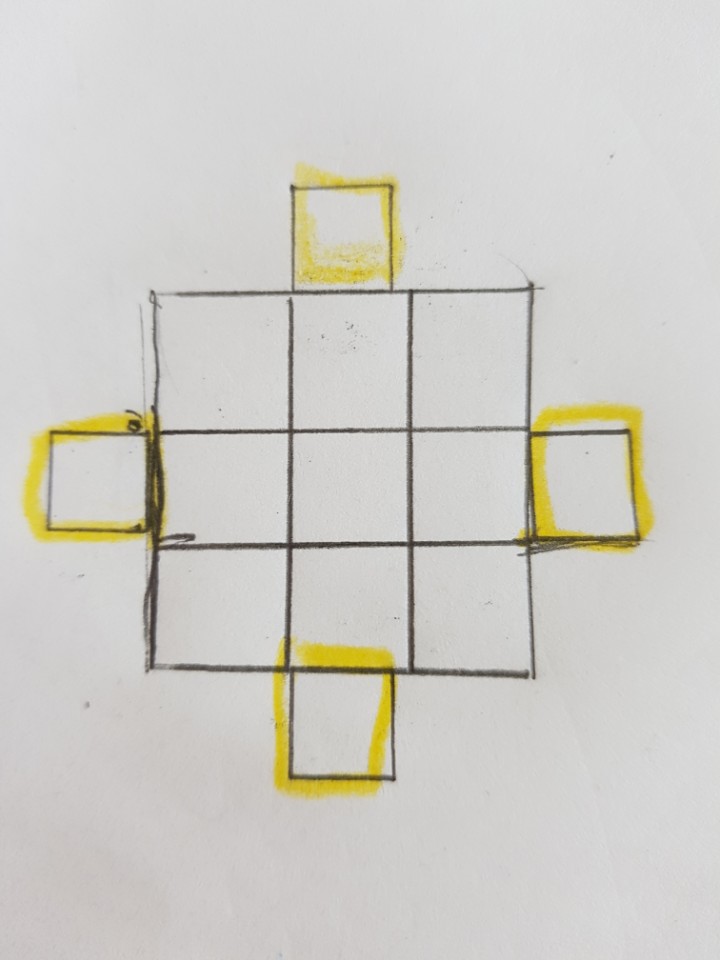
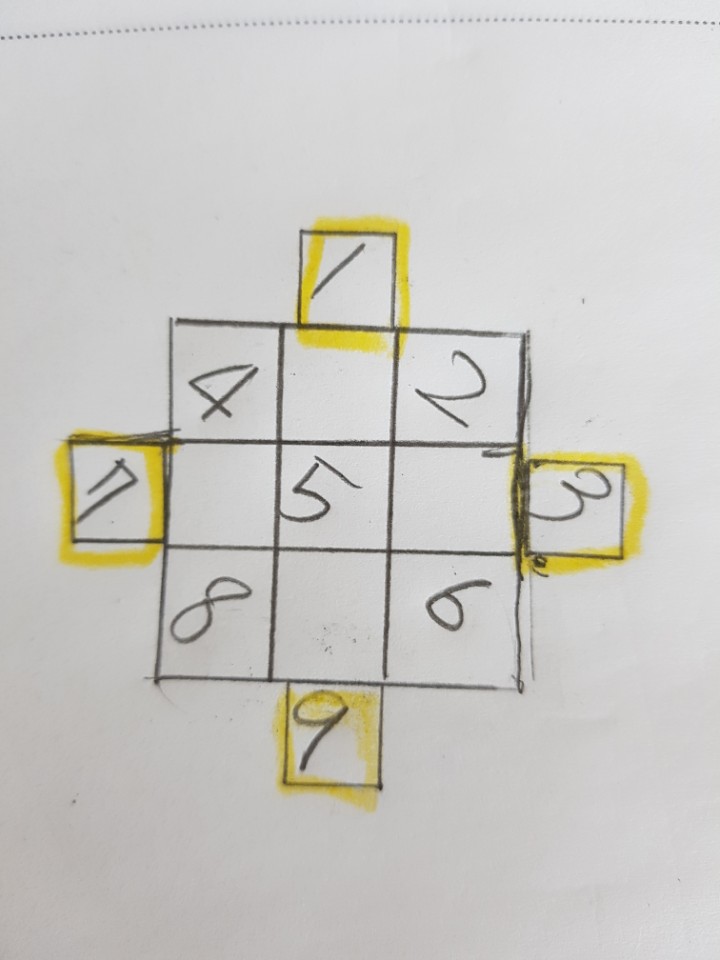
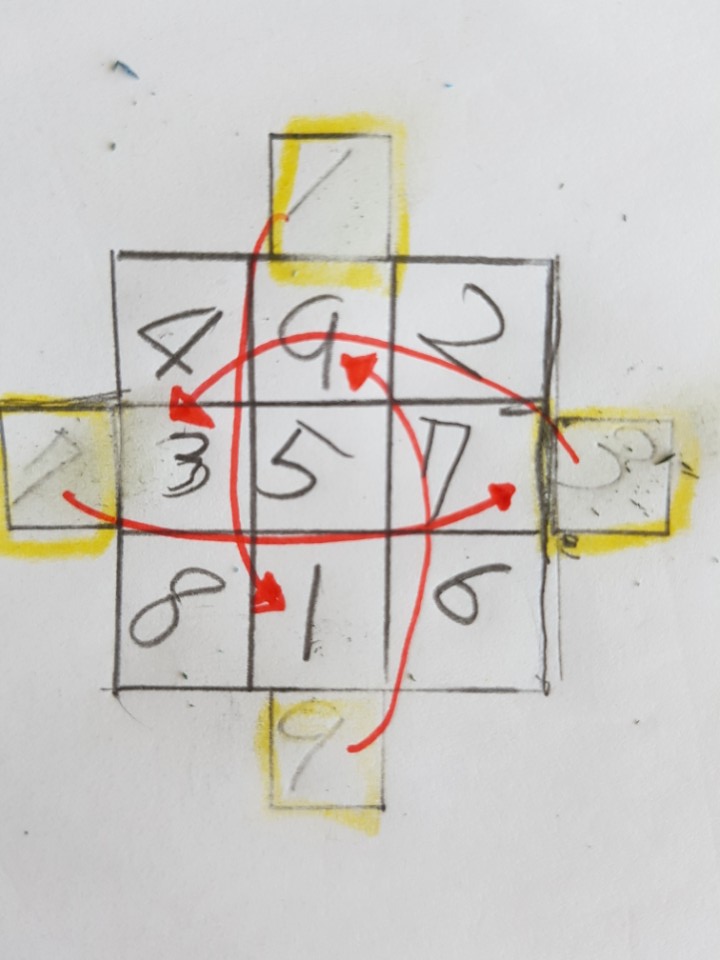
짝수 마방진을 만드는 방법을 알려드리겠습니다. 짝수 마방진은 모스 헤르둔트 수열법이라는 것인데요. 이 방법은 4의 배수일때 칸의 수를 1:2:1 비율로 나뉜다는 것을 이용한 것입니다. 밝은 색으로 표시된 영역을 정방향으로 숫자를 써넣고 나머지 영역 끝에서부터 역방향으로 숫자를 빈칸을 다 채웁니다.

이렇게 하여 4차 마방진을 만들 수 있습니다.

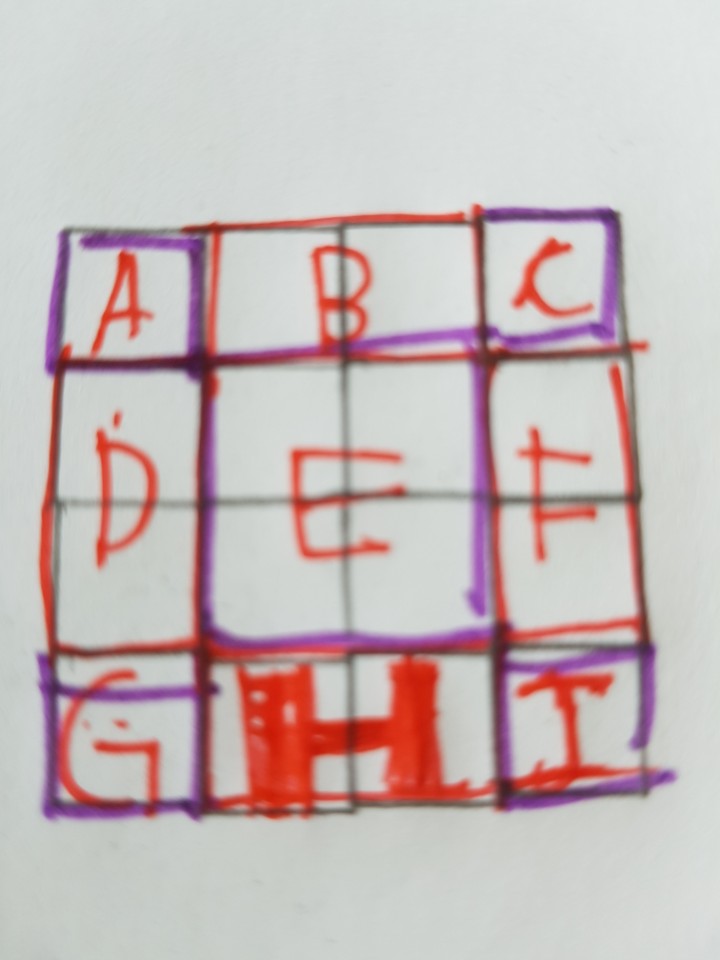
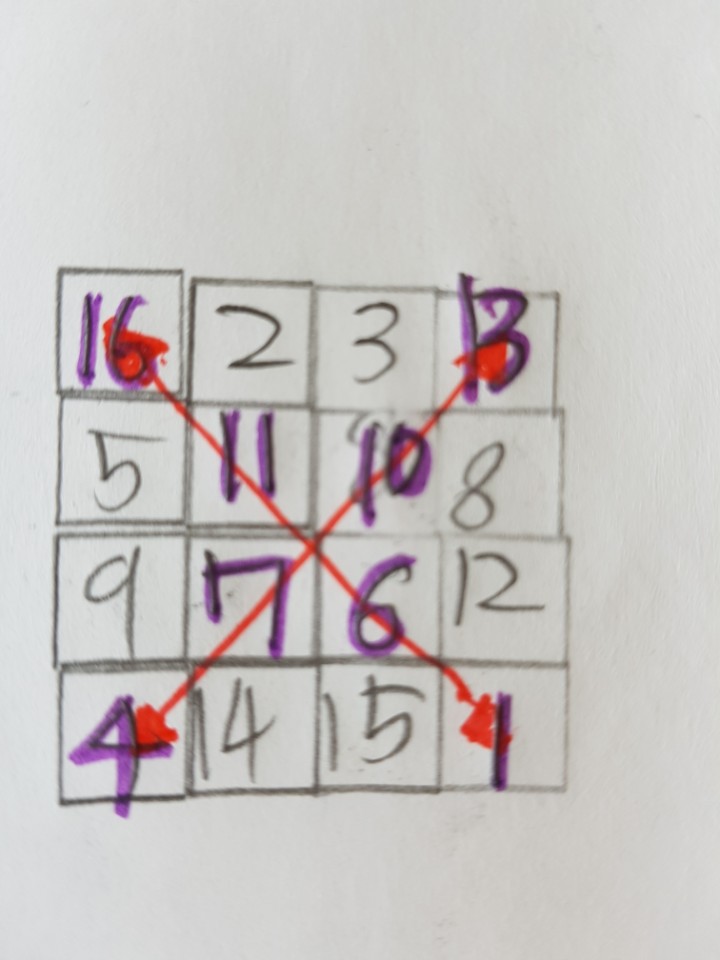
그리고 다음에는 마방진 속의 마법수를 구하는 것인데요~ 마법수는 서양의 수학자들이 마방진을 연구하는데 있어서 필요한 숫자인데요. 위 아래로 세칸을 다 더하여 있는 칸들의 수를 다 합한 것이 마법수라고 할 수 있습니다. 3차 마방진에서는 마법수가 15가 나옵니다. 마법수는 들어가는 수들을 다 더한 후 겹치는 수만큼 곱한 후 1,2,3,4,5,6,7,8,9를 다 더한후 겹치는 수 2 곱한후 90 마법수가 포함되는 변의수(대각선을 포함하지 않음) 즉, 3차 마방진에서는 6으로 나누면 15가 됩니다.

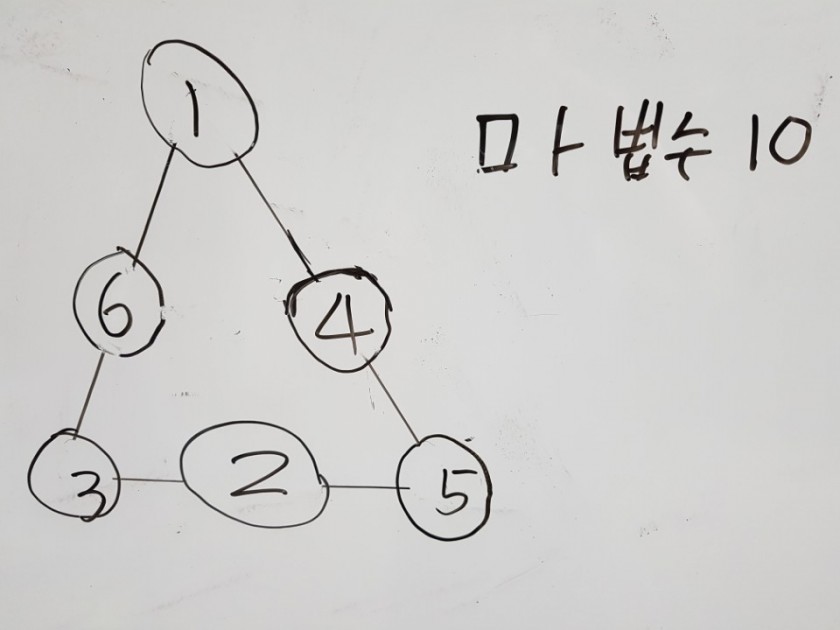
마방진의 종류라고 하기는 그렇지만 마방진의 친척인 형진을 알아보겠습니다. 종류에는 테두리 방진, 삼각진, 육각진, 원형진 등이 있는데요. 너무 많으니 간단한 것만 설명하겠습니다. 첫 번째 설명할 것은 테두리 방진 중 삼각진인데요. 삼각진은 삼각형처럼 생겨서 삼각진이라고 합니다. 1부터 6까지 숫자를 넣어서 다음과 같이 삼각진을 만들어 보았습니다. 간단한 삼각진입니다.

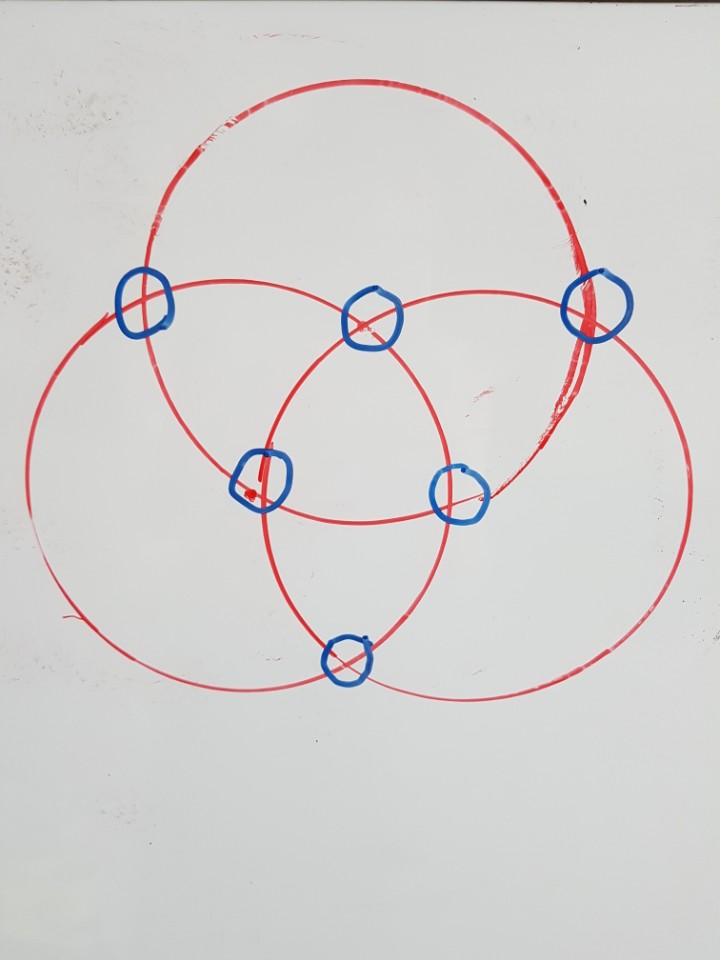
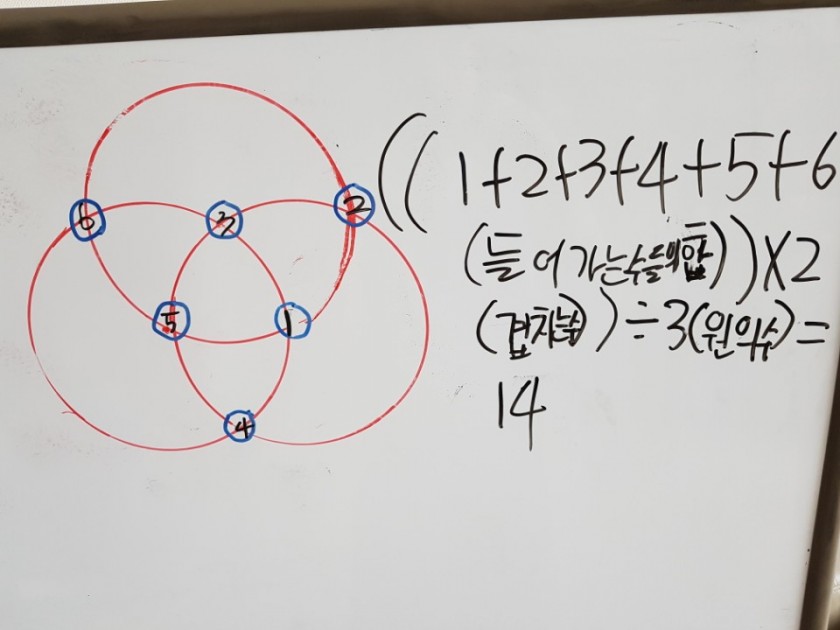
다음은 원형진입니다. 원형진은 원과 원이 만나는 점에 숫자를 써넣어 만든 마방진인데요. 이 마방진은 원에있는 숫자가 네 개일 경우에는 마법수가 14로 만드는 원형진입니다.

1+2+3+4+5+6 =21

21*2= 42(겹치는 수 곱하기)

그 다음 포함되는 변만큼 나누면 3개의 원으로 나누면 42/3=14

14에 맞춰서 원에 숫자를 채워나가면 되는 것이지요.

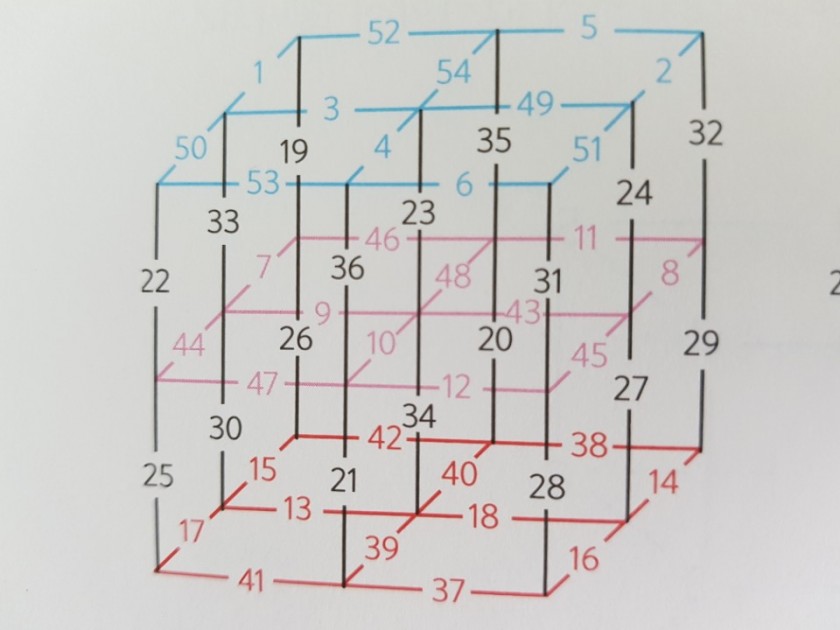
마지막으로 정육면체 마방진인 정육면체 진입니다. 정육면체 진은 입체도형으로 만들었는데요. 입체 도형은 만들기도 어렵고 더하기도 어렵기 때문에 컴퓨터로 마방진을 만든다고 합니다.

그리고 마방진을 연구했던 우리나라 최고수학자 최석정의 구술약에 나오는 방사형진이 있는데요 방사형진은 원 안에 있는 수들의 합이 모두 같고 그리고 줄 위에 있는 수들의 합이 모두 같은 방사형진입니다. 이 방사형진은 쉽게 만들면 아주 쉽지만 어렵게 만들면 아주 여려운 마방진입니다.

이렇게 마방진 친척들을 알아보았습니다.

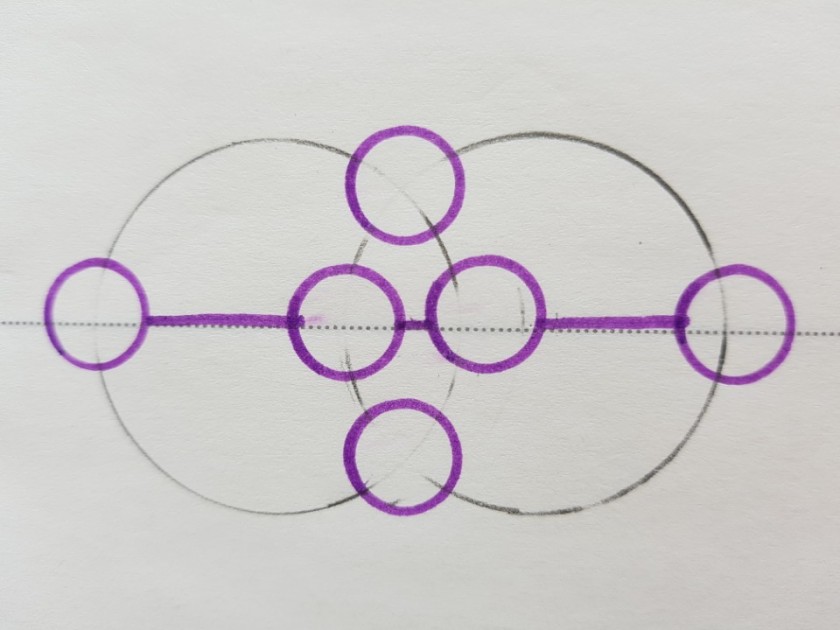
마지막으로 방사형진에 대한 퀴즈를 하나 내겠습니다.

아래와 같은 모양인데요!

퀴즈

1부터 6까지의 숫자를 넣어서 아래 원에 놓인 숫자의 합과

선분에 놓인 숫자의 합이 같아지도록 하시오 

-----

<정답>

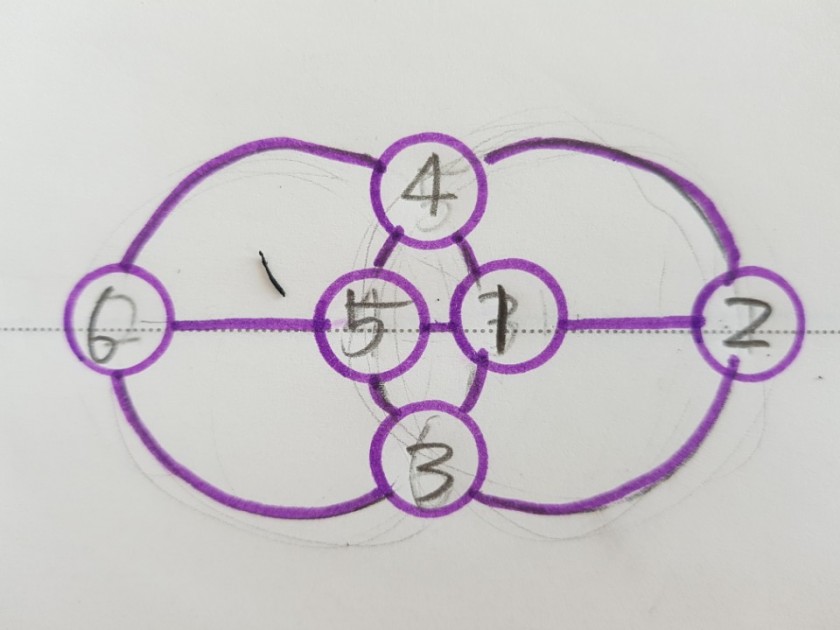
저는 이 마방진을 공부하면서 재미있는 수학퍼즐이 있다는 것을 알았습니다.

또한, 이런 것이 생활에서도 쓰이면 도움이 될 것 같다는 생각이 듭니다.

이상 세종시 이우혁 기자였습니다.