어린이과학동아&수학동아 기사
정오각형으로 테셀레이션을 만들 수 없는 이유는?
안녕하세요,이경환 기자입니다. 오늘은 우리 주변에서도 볼 수 있는 테셀레이션에 대해서 알아보고 정오각형은 왜 테셀레이션이 될 수 없는지 알아보도록 하겠습니다.(일러두기:출처가 공개되지 않은 사진은 직접 촬영한 사진입니다.)

출처:네이버 블로그
1.테셀레이션
순우리말로는 쪽매맞춤,쪽매붙임이라고 불리는 테셀레이션은 평면도형을 겹치지 않으면서 빈틈이 없게 모으는 것을 의미합니다. 평면도형을 뒤집거나 돌릴 수 있어 다양한 문양을 만들 수 있어 보도블럭 등 다양한 곳에 쓰이고 있습니다.

또 이것을 그림에 이용해 그림을 그려낸 유명한 화가,에셔도 있습니다.

출처:네이버 블로그
2.정다각형 테셀레이션의 원리
이제 정오각형이 왜 테셀레이션이 되지 않는지 확인해보도록 하겠습니다. 우리가 보도블럭 등 흔히 보고 알고 있는 테셀레이션은 대부분 정규 테셀레이션이므로 이것을 기준으로 하고 생각해 보도록 하겠습니다.
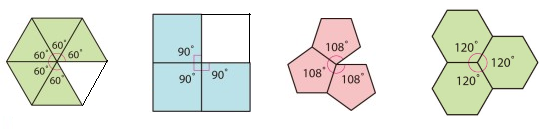
출처:네이버 블로그
그림을 보시면 정규 테셀레이션이 가능한 정삼각형,정사각형,정육각형은 모두 한 꼭짓점에서의 각이 모두 360도 인 것을 알 수 있습니다. 하지만 유일하게 정오각형은 324도로 360도가 되지 않는 것을 볼 수 있습니다. 즉 정오각형만으로는 빈틈을 다 채울 수 없고 이 때문에 정오각형로 정규 테셀레이션을 할 수 없습니다.
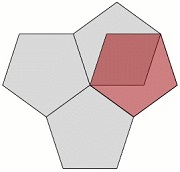
출처:네이버 블로그
3.이외의 방법
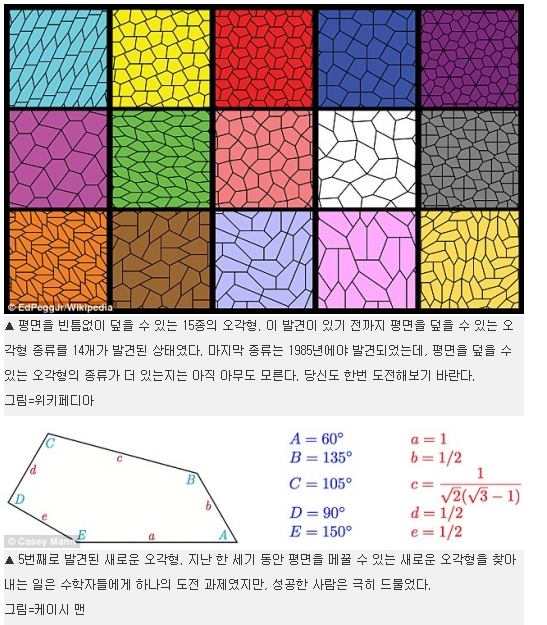
출처:네이버 블로그
그러나 정오각형이 아닌 오각형으로는 테셀레이션을 만들 수 있습니다. 위 사진처럼 15가지 뿐이라고 합니다. 다른 도형보다 훨씬 적은 경우의 수를 가지고 있습니다. 오각형 테셀레이션의 발견은 수학에서 매우 어려운 난제로 14번째 경우의 수를 찾은 것이 1985년으로 무려 30년 후인 2015년이 되서야 3명의 수학자들이 15번째 경우의 수를 찾아냈다고 합니다. 그 만큼 오각형으로 테셀레이션을 만들기란 매우 힘든 일이라는 것이죠. 지금 16번째 오각형 테셀레이션이 발견된다면 수학사에 길이 남을 발견이 될 것이라고 합니다.(새로운 행성을 찾은 급의 발견이라고 생각하면 될 듯)
어떠셨나요? 우리 주변에도 테셀레이션이 아주 많이 있었고 이것에도 수학적 이론이 스며들어져 있었습니다. 여러분도 주변에서 테셀레이션을 찾아보시면 좋을 것 같습니다.
글쓰기 평가어린이과학동아 기자2021.11.01
<정오각형으로 테셀레이션을 만들 수 없는 이유는?>이라는 제목으로 수학 기사를 써 주었네요. 다소 어려울 수 있는 개념인데, 원리 그림과 적절한 예를 통해 쉽게 소개하려고 노력해 주었어요. 테셀레이션의 개념, 그리고 정오각형으로 테셀레이션을 만들 수 없는 이유를 잘 설명해 주었는데요. 오각형으로는 테셀레이션을 만들 수 있다는 부분은 꽤 어렵기도 하고, 경환 기자가 자신의 말로 이해하고 소개했다기 보다는 자료를 참고해서 정리해 주었기 때문에 좀 더 쉽게 이해하기 쉽도록 풀어서 소개해 주면 좋을 것 같네요.

마지막으로